Obliczanie belek

Obliczanie belek – w statyce i mechanice oznacza przeprowadzenie obliczeń w celu wyznaczenia reakcji podpór oraz sił wewnętrznych i narysowaniu wykresów. Obliczanie belek polega na:

• sprawdzeniu statycznej wyznaczalności i geometrycznej niezmienności,
• obliczeniu reakcji podpór,
• wyznaczeniu sił wewnętrznych.
• narysowaniu wykresów.

Poprzez siły wewnętrzne należy rozumieć: momenty zginające, siły tnące i siły osiowe (normalne).

1. Określenie statycznej wyznaczalności i geometrycznej niezmienności

Przed rozpoczęciem obliczania belek należy sprawdzić czy daną belkę da się rozwiązać – tzn czy zachowane zostały odpowiednie proporcję pomiędzy liczbą tarcz a liczbą więzi elementarnych. Ważne jest też czy zostały one odpowiednio wykorzystane. Szczegółowo opisałem to tutaj statyczna wyznaczalność i geometryczna niezmienność. W skrócie i uproszczeniu: jeśli liczba więzi jest trzykrotnie większa niż liczba tarcz można iść dalej.

Dla układu jak powyżej: liczba tarcz = 1, liczba więzi = 3. Korzystając ze wzoru e = 3t otrzymamy, że 3=3, a więc układ jest statycznie wyznaczalny. Układ jest również geometrycznie niezmienny (twierdzenie o dwóch tarczach).

2. Obliczenie reakcji podpór

Nasza belka jest przymocowana do fundamentu za pomocą podpór. Reakcje jakie powstają w belce zależą od rodzaju podpory, którą belka jest przymocowana do fundamentu – np  w przypadku belki swobodnie podpartej powstają 3 reakcje (dwie pionowe i jedna pozioma – najczęściej reakcja pozioma jest zerowa gdyż nie działają siły od której mogłaby powstać).

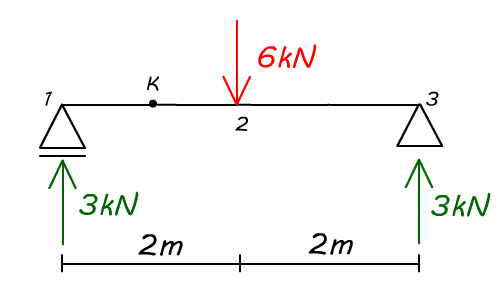
Reakcje w belce można obliczyć układając równania korzystając z trzech podstawowych warunków:

• ΣM_i = 0. Suma wszystkich momentów względem dowolnego punktu na belce powinna wynosić 0. Bez względu na punkt względem którego będziemy układać równanie, wszystko musi się zsumować do zera;

ΣM_K = 0
3kN · 1m + 6kN · 1m – 3kN · 3m = 0
3kNm + 6kNm – 9kNm = 0
0 = 0

• ΣY = 0. Suma rzutów wszystkich sił względem osi Y musi się równań 0. Jeśli dodamy do siebie wszystkie siły pionowe to powinny się one zsumować do zera;

ΣY = 0
-3kN + 6kN – 3kN = 0
0 = 0

• ΣX = 0. Suma rzutów wszystkich sił względem osi X musi się równań 0. Jeśli dodamy do siebie wszystkie siły poziome to powinny się one zsumować do zera (podobnie jak siły pionowe);

3. Wyznaczenie sił wewnętrznych

Najważniejszym elementem obliczania belek jest prawidłowe wyznaczenie momentów zginających. Sposób ich wyznaczania, krok po kroku możesz znaleźć tu: belka swobodnie podparta.

Istotą rolę pełnią również siły tnące – siły powstające w wyniku działania sił w płaszczyźnie pionowej (Y). Sposób wyznaczania sił tnących opisałem np przy okazji obliczania belki złożonej.

W belkach występują jeszcze siły osiowe – siły powstające w wyniku działania sił w płaszczyźnie poziomej (X). Ich wyznaczanie jest analogiczne do sił tnących.

4. Narysowanie wykresów

Elementem końcowym obliczania belek jest narysowanie wykresów sił wewnętrznych – zwłaszcza momentów zginających. Przy rysowaniu wykresów momentów zginających należy pamiętać o najważniejszej zasadzie: wykresy momentów odkłada się po stronie włókien faktycznie rozciąganych. Jednostką momentów zginających jest kNm.

Wykresy sił tnących oznacza się literą “T”, ich jednostką jest kN. Właściwie nie ma znaczenia po której stronie wykresu odłoży się wykres sił tnących – istotny jest jednak znak. Stąd na wykresach przy siłach tnących pojawia się znak “+” lub “-“. Podobnie jest z siłami osiowymi, które oznacza się literą “N”. W przypadku gdy sił osiowe (normalne) wynoszą zero, wystarczy narysować prostą i na środku wpisać 0. Więcej o wykresach sił wewnętrznych.

Przykłady obliczeniowe

Przykłady obliczania belek, zarówno tych prostych jak i złożonych, znajdziesz w dziale “belka“. Naukę najlepiej rozpocząć od belki swobodnie podpartej. Powodzenia!