Belka prosta z łyżwą

Belka prosta z jednej strony podparta łyżwą pionową, z drugiej strony podporą przegubowo-przesuwną, obciążona do połowy obciążeniem równomiernie rozłożonym.

1. Statyczna Wyznaczalność i Geometryczna niezmienność

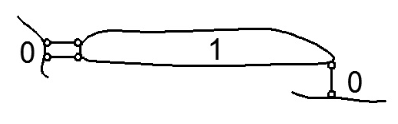
Jest to belka prosta więc mamy tylko jedną tarczę połączoną z fundamentem za pomocą trzech więzi.

Liczba więzi e=3
Liczba tarcz t=1

e = 3t
3 = 3 · 1
3 = 3

Układ jest statycznie wyznaczalny.

Układ z racji rodzaju podpór jest geometrycznie chwilowo zmienny, więc nie będziemy sprawdzać geometrycznej niezmienności. Nie oznacza to jednak, że nie da się go rozwiązać – rozwiążemy go gdyż jest to ciekawy przykład obliczeniowy.

2. Reakcje podpór

W podporze typu łyżwa powstają dwie reakcje pozioma oraz moment. Reakcję poziomą można pominąć w obliczeniach gdyż nie ma żadnej siły od której mogłaby powstać (nie działa żadna siła pozioma lub pod kątem). Skupimy się więc tylko na reakcji momentu M1 i reakcji V2. Zacznijmy od momentu M1. W tym celu najlepiej ułożyć równanie sumy momentów względem punktu 2.

ΣM₂ = 0
– 2kN/m · 2m · 3m + M1 = 0
– 12kNm + M1 = 0
M1 = 12kNm

Reakcje V2 policzymy korzystając z warunku, że suma wszystkich sił względem osi Y musi wynosi 0.

ΣY = 0
2kN/m · 2m – V2 = 0
V2 = 4kN

Sprawdzenie poprawności obliczonych reakcji. W tym przykładzie może wydawać się to zbędne ale dla własnej kontroli i wyrobienia sobie dobrych nawyków warto ją przeprowadzić. Sprawdźmy poprawność obliczonych reakcji układając równanie sumy momentów względem punktu A (środka belki).

ΣM_A = 0
12kNm – 2kN/m · 2m · 1m – V2 · 2m = 0
12kNm – 4kNm – 4kN · 2m = 0
12kNm – 4kNm – 8kNm = 0
0 = 0

Reakcje policzone prawidłowo.

3. Siły przekrojowe

3.1 Momenty zginające

Z obliczeniami będziemy szli z lewej strony do prawej. Z racji tego, że na przedziale 1-A działa obciążenie równomiernie rozłożone, musimy ułożyć równanie momentu.

Przedział 1-A

M(x) = 12 – 2 · x · 0,5 · x
M(x) = 12 – x²

Ekstremum

M'(x) = -2x
0 = -2x
x = 0

Ekstremum znajduje się zatem na końcach przedziału.

Punkt 1, x = 0m

M(x) = 12 – x²
M(0) = 12kNm

Punkt A, x = 2m

M(x) = 12 – x²
M(2) = 12 – 2²
M(2) = 8kNm

Punkt 2

Na przedziale A-2 wykres będzie liniowy. Wystarczy więc, że obliczymy moment w punktach charakterystycznych. Moment w punkcie A mamy już policzony. Został tylko punkt 2. Tutaj z racji tego, że punkt znajduje się na końcu belki moment będzie wynosił 0.

M2 = 0

3.2 Siły tnące

Przedział 1-A

T(x) = M'(x) = -2x

Punkt 1, x = 0m

T(x) = -2x
T(x) = 0

Punkt A, x = 2m

T(x) = -2x
T(2) = -4kN

Przedział A-2

T_A-2 = -4kN

3.3 Siły osiowe

W całej belce siły osiowe wynoszą zero, z racji braku działania sił poziomych.

4. Wykresy sił przekrojowych

Na odcinku 1-A (od wartości 12kNm do 8kNm) wykres to krzywa drugiego stopnia (parabola). Belka z łyżwą pionową policzona!