Metoda Rittera – sposób obliczania sił wewnętrznych w kratownicy polegający na przecięciu kratownicy na dwie części i obliczeniu sił w przeciętych prętach. Taki sposób rozwiązywania kratownicy nazywany jest też metodą przecięć. Metoda Rittera polega na przecięciu kratownicy w taki sposób aby:
- przeciąć 3 pręty,
- w odciętych częściach kratownicy były co najmniej dwa węzły,
- pręty nie wychodziły z tego samego węzła.
Przykładowa kratownica przecięta metodą Rittera:

Metoda Rittera znacząco upraszcza rozwiązywanie kratownic i jest zdecydowanie najszybszą analityczną metodą rozwiązywania kratownic, zwłaszcza gdy należy wyznaczyć siłę osiową w konkretnym pręcie. W metodzie Rittera dla każdej odciętej części kratownicy spełnione są warunki:
- suma momentów względem dowolnego punktu wynosi 0 (ΣM = 0),
- suma wszystkich sił względem osi Y (siły pionowe) wynosi 0 (ΣY = 0),
- suma wszystkich sił względem osi X (siły poziome) wynosi 0 (ΣX = 0).
Metoda Rittera – przykład obliczeniowy

1. Statyczna wyznaczalność geometryczna niezmienność
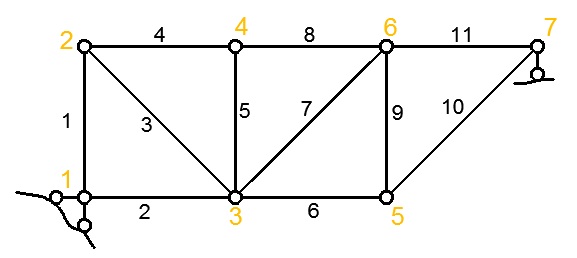
Liczba węzłów w = 7
Liczba prętów r = 11
Liczba reakcji r = 3
2w = p + r
2 · 7 = 11 + 3
14 = 14
Warunek spełniony – układ jest statycznie wyznaczalny.
Kratownica ma klasyczną budowę trójkątną. Układ jest geometrycznie niezmienny.
2. Wyznaczenie reakcji podpór

Reakcje w kratownicy wyznaczamy w identyczny sposób jak w ramach.
ΣM1 = 0
6kN · 2m – 2kN · 2m + 4kN · 4m – V7 · 6m = 0
12kNm – 4kNm + 16kNm – V7 · 6m = 0
24kNm – V7 · 6m = 0
V7 · 6m = 24kNm
V7 = 4kN
ΣY = 0
– V1 – 2kN + 4kN – V7 = 0
– V1 – 2kN + 4kN – 4kN = 0
– V1 – 2kN = 0
V1 = – 2kN
ΣX = 0
H1 + 6kN = 0
H1 = – 6kN
Sprawdzenie:
ΣM4 = 0
V1 · 2m – H1 · 2m + 4kN · 2m – V7 · 4m = 0
– 2kN · 2m + 6kN · 2m + 4kN · 2m – 4kN · 4m = 0
– 4kNm + 12kNm + 8kNm – 16kNm = 0
0 = 0
Reakcje policzone poprawnie.
3. Siły przekrojowe
Ponieważ z założenia wynika, że w kratownicy momenty i siły tnące wynoszą zero, będziemy liczyć tylko siły osiowe.

Zanim jednak przejdziemy do obliczeń określmy które pręty będą prętami zerowymi. Jeśli takie znajdziemy będziemy mięli mniej pracy. W naszym przypadku prętem w którym siły osiowe wynoszą zero będzie pręt 3-4.
By wyznaczyć siły osiowe w kratownicy będziemy stosowali metodę Rittera (przecięć). Polega ona na przecinaniu kratownicy i obliczaniu sił osiowych w przeciętych prętach. Przeciąć kratownicę można tylko w taki sposób aby:
– po każdej stronie cięcia były co najmniej dwa węzły,
– przeciąć 3 pręty,
– pręty nie wychodziły z tego samego węzła.
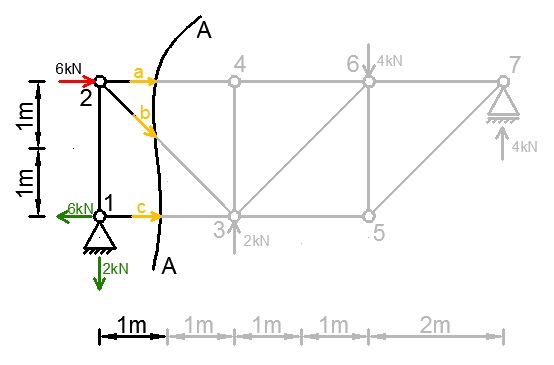
Po przecięciu kratownicy trzeba pamiętać, że zajmujemy się siłami tylko po jednej stronie cięcia. Pozostałe nas nie interesują. Obliczając momenty względem punktów kratownicy będziemy wyznaczać interesujące nas wartości a, b i c. Znakowanie zgodnie z zasadą zegara.
Wybieramy taki punkt (węzeł) w którym zbiegają się nasze dwie niewiadome.
ΣM2 = 0
6kN · 2m – c · 2m = 0
12kNm – c · 2m = 0
c = 6kN
Kolejny punkt, w którym zbiegają się dwie niewiadome to punkt 3. To, że znajduje się on poza cięciem nie ma znaczenia. Chodzi po prostu o dowolny punkt na płaszczyźnie.
ΣM3 = 0
– 2kN · 2m + 6kN · 2m + a · 2m = 0
– 4kNm + 12kNm + a · 2m = 0
8kNm + a · 2m = 0
a = – 4kN
Żeby policzyć siłę osiową b, musimy rozłożyć ja na składową poziomą i pionową.

Wystarczy obliczyć tylko jedną z niewiadomych bx lub by. Następnie za pomocą funkcji trygonometrycznych obliczy się wartość b. Przy obliczaniu pamiętajmy, żeby nie uwzględniać wartości b, ponieważ zastąpiliśmy ją składowymi bx i by.
ΣM1 = 0
6kN · 2m + bx · 2m + a · 2m = 0
12kNm + bx · 2m – 4kN · 2m = 0
12kNm + bx · 2m – 8kNm = 0
4kNm + bx · 2m = 0
bx = -2kN
Pręt jest pod kątem 45º, zatem otrzymaną wartość musimy pomnożyć razy √2
b = bx · √2
b = -2√2kN
Żeby policzyć siły w kolejnych prętach potrzebujemy przeciąć kratownicę kolejny raz.

ΣM3 = 0
– 2kN · 2m + 6kN · 2m + d · 2m = 0
– 4kNm + 12kNm + d · 2m = 0
8kNm + d · 2m = 0
d = -4kN
ΣM6 = 0
6kN · 2m – 2kN · 4m + 2kN · 2m – f · 2m = 0
12kNm – 8kNm + 4kNm – f · 2m = 0
8kNm – f · 2m = 0
f = 4kN
By policzyć wartość e moglibyśmy postępować w identyczny sposób jak przy wyznaczaniu siły b. Pokażę Wam jednak inny sposób, w który można obliczyć siłę w prętach ukośnych. Korzystamy tu z faktu, że nasza kratownica zbudowana jest z “kwadratów” o boku 2m.
Przekątna naszych kwadratów to 2√2m. Jej połowa czyli ramię na jakim będzie działać siła e to √2m.
ΣM5 = 0
– 2kN · 4m + 2kN · 2m + 6kN · 2m + d · 2m + e · √2m = 0
– 8kNm + 4kNm + 12kNm – 4kN · 2m + e · √2m = 0
– 8kNm + 4kNm + 12kNm – 8kNm + e · √2m = 0
0 + e · √2m = 0
e =0
Kolejne siły osiowe wyznaczone. I tak aż do końca, aż obliczy się wszystkie siły w prętach. Dla treningu spróbuj samodzielnie wyznaczyć pozostałe siły w prętach metodą przecięć. Spróbuj nie korzystać z innych metod (np. równoważenia węzłów). Pamiętaj, że dla takiej odciętej części kratownicy prawdziwe są również warunki, że ΣX = 0 jak i ΣY = 0. Na pewno ułatwi Ci to obliczenia.
4. Wykresy sił przekrojowych

Jak widać obliczanie sił osiowych w kratownicy nie jest trudne. Wystarczy kilka cięć i kratownica rozwiązania. Powodzenia z trudniejszymi kratownicami!
