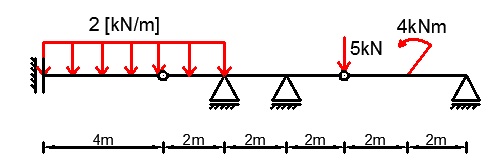
1. Statyczna wyznaczalność i geometryczna niezmienność

Liczba więzi e = 9 (przegub pomiędzy dwiema tarczami odbiera dwa stopnie swobody)
Liczba tarcz t = 3
e = 3t
9 = 3 · 3
9 = 9
Warunek spełniony, układ jest statycznie wyznaczalny.
W tym przykładzie nie będziemy jednak sprawdzać geometrycznej niezmienności. Jest to układ geometrycznie chwilowo zmienny (z racji połączenia tarczy 1). Jest to jednak dobry przykład do poćwiczenia więc przejdziemy od razu do obliczenia reakcji podpór.
2. Wyznaczenie reakcji podpór

Przy obliczaniu reakcji korzystamy z faktu, że moment w przegubie zawsze jest równy zero. Z tego wynika, że suma momentów po dowolnej stronie przegubu też jest równa zero. Policzmy reakcję V7.
ΣM5P = 0
-4kNm – V7 · 4m = 0
V7 · 4m = – 4kNm
V7 = -1kN
By policzyć reakcje V3 i V4 musimy ułożyć układ równań. Skorzystamy z warunków:
1) ΣY = 0
2kN/m · 6m – V3 – V4 + 5kN – V7 = 0
12kN – V3 – V4 + 5kN – (-1kN) = 0
V3 + V4 = 18kN
2) ΣM2P = 0
2kN/m · 2m · 1m – V3 · 2m – V4 · 4m + 5kN · 6m – 4kNm – V7 · 10m = 0
4kNm – V3 · 2m – V4 · 4m + 5kN · 6m – 4kNm + 1kN · 10m = 0
–V3 · 2m – V4 · 4m + 40kNm = 0
V3 · 2m + V4 · 4m = 40kNm
Mamy teraz taki oto układ równań:
V3 + V4 = 18
V3 · 2 + V4 · 4 = 40
Możemy go rozwiązać ręcznie lub skorzystać z jednego z dostępnych programów online do rozwiązywania układów równań. Po rozwiązaniu otrzymujemy następujące wyniki:
V3 = 16kN
V4 = 2kN
Wszystkie reakcje pionowe mamy już policzone. Policzmy teraz moment w łyżwie.
ΣM2L = 0
M1 – 2kN/m · 4m · 2m = 0
M1 – 16kNm = 0
M1 = 16kNm
Reakcja pozioma H1 będzie równa zero.
H1 = 0
Sprawdzenie: Gdy układ jest rozbudowany, a obliczeń było sporo warto sprawdzić czy reakcje policzyliśmy poprawnie. Obliczamy moment w dowolnym punkcie belki. Moment powinien wyjść zero.
ΣM6 = 0
M1 – 2kN/m · 6m · 9m + V3 · 6m + V4 · 4m – 5kN · 2m – 4kNm – V7 · 2m = 0
M1 – 2kN/m · 6m · 9m + 16kN · 6m + 2kN · 4m – 5kN · 2m – 4kNm + 1kN · 2m = 0
16kNm – 108kNm + 96kNm + 8kNm – 10kNm – 4kNm + 2kNm = 0
0 = 0
Reakcje policzone poprawnie
3. Siły przekrojowe
Po naniesieniu reakcji i oznaczeniu włókien porównawczych belka wygląda tak:

3.1 Momenty zginające
Punkt “1”
Mamy łyżwę, więc moment na podporze nie będzie zerowy.
M1 = 16kNm
Przedział “1-3”
Ze względu na obciążenie rozłożone musimy ułożyć równanie.
M(x) = 16kNm – 2kN/m · xm · 0,5 · xm
M(x) = 16 – x2
Równanie gotowe, czas określić ekstremum
M(x) = 16 – x2
M'(x) = -2x
0 = -2x
x = 0
A więc ekstremum momentu jest w miejscu gdzie x = 0m czyli na łyżwie
M(x) = 16 – x2
M(0) = 16kNm
M1 = 16kNm
Wszystko się zgadza. Sprawdźmy teraz czy w przegubie wyjdzie nam moment zerowy (x = 4m)
M(x) = 16 – x2
M(4) = 16 – 42
M(4) = 0
M2 = 0
Policzmy jeszcze moment na końcu przedziału, czyli w punkcie 3.
M(x) = 16 – x2
M(6) = 16 – 62
M(6) = – 20kNm
M3 = -20kNm
Punkt “4”
Nie musimy układać równania. Obciążenie rozłożone traktujemy już jako całość.
M4 = 16kNm – 2kN/m · 6m · 5m + 16kN · 2m
M4 = 16kNm – 60kNm + 32kNm
M4 = -12kNm
Punkt “5”
Ponieważ jest to przegub moment będzie równy zero
M5 = 0
Punkt “6”
Rozpatrzymy dwa przypadki. Najpierw obliczamy moment z lewej strony punktu nie uwzględniając momentu zadanego 4kNm. W drugim przypadku uwzględnimy ten moment.
M6L = 16kNm – 2kN/m · 6m · 9m + 16kN · 6m + 2kN · 4m – 5kN · 2m
M6L = 16kNm – 108kNm + 96kNm + 8kNm – 10kNm
M6L = 2kNm
M6P = 16kNm – 2kN/m · 6m · 9m + 16kN · 6m + 2kN · 4m – 5kN · 2m – 4kNm
M6P = 16kNm – 56kNm + 96kNm + 8kNm – 10kNm – 4kNm
M6P= -2kNm
Punkt “7”
Moment w tym punkcie wynosi zero. Jest to koniec naszej belki.
M7 = 0
3.2 Siły tnące

Przedział “1-3”
Siły tnące to pierwsza pochodna momentu. Równanie momentu już mamy, ułożyliśmy je wcześniej.
M(x) = 16 – x2
M'(x) = -2x
T(x) = -2x
Policzmy siłę tnącą na końcach przedziałów.
T(x) = -2x
T(0) = 0
T(x) = -2x
T(6) = -12kN
Przedział 3-4
Dochodzi nam siła pionowa z reakcji.
T3-4 = -12kN + 16kN
T3-4 = 4kN
Przedział 4-5
Uwzględniamy kolejną reakcję.
T4-5 = 4kN + 2kN
T4-5 = 6kN
Przedział “5-7”
Dochodzi nam siła pionowa 5kN.
T5-6 = 6kN – 5kN
T5-6 = 1kN
Punkt “7”
Na końcu naszej belki, w punkcie 7, działa reakcja skierowana pionowo w dół o wartości 1kN. Jak widać zniosą się, czyli możemy przypuszczać, że siły tnące policzyliśmy poprawnie.
T = 1kN – 1kN
T = 0
3.3 Siły osiowe.
Siły osiowych brak w naszym układzie, nie ma żadnych reakcji poziomych.
4. Wykresy sił przekrojowych



